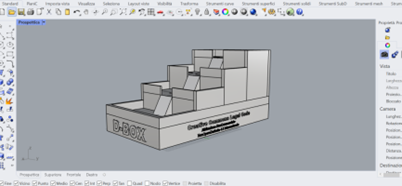
D-Box is a 3D printing game to convert a decimal number into a binary number, to realize this, it offers a configuration of a set of platform based on the powers of 2 [7]. D-BOX connects some disciplines: mathematic, information technologies and media education; it provides a way to show how mathematic is essential and necessary to the modern digital world. This game is based on two concepts already studied in the fifth grade of primary school: 1) mathematical operations knowledge (computing) 2) recognizing geometric figures [21]. The teacher gives a number of marbles to the student that has to place on platforms in a proper way to give back a digital number composed just with 0 or 1 digit.
D-BOX 3D model ready to be printed.
B-BOX and Ames Room Tests at “G.Rodari” Primary School
of Perugia
These Open Education resources perform, hopefully, a stimulating contribution to 3D
printing projects in Italian schools. Usually, the Minister of Education intends to promote
the adoption of innovative teaching methodologies by schools, with particular reference
to digital teaching and STEAM disciplines (Science, Technology, Engineering, Arts
and Mathematics), inspired by students’ leadership, active learning and cooperative,
to relational well-being, in line with the “Skills and Contents” area of the National
Plan for the digital school (30 April 2021, n. 147) and many schools buy 3D printer but,
unfortunately, often they are “parked” in a laboratory because there is no project to follow
and/or adequate training of the teaching staff. The impact of the solutions developed by
Lab-H would help this staff in order to improve the digital skills of teachers and students.
This impact will be better highlighted with some data. Lab-H in collaboration with
“G.Rodari” primary school of Perugia tested D-BOX and Ames Room in this academic
year 2020–21, and it will test also Montessori didactical object in the next academic year
2021–22. About D-BOX, usually to convert decimal number into binary number an easy
algorithm is this: 1) divide the decimal number by two; 2) write the integer quotient to be
used int next iteration; 3) write the remainder that is the binary digit; 4) repeat until the
quotient is equal to zero. Vice versa (the reverse algorithm), to convert a binary number
(such as a four bit number Bit3 Bit2 Bit1 Bit0) in its decimal number must be add binary
digits Bitn times their power of 2. This procedure is quite hard for students that are some
gaps in mathematical or students less motivated to activate mathematical intelligence, in
terms of Gardner’s theory of multiple intelligences [19]. Students (15 students composed
by 12 males, 3 females), not helping by teacher, in classroom: 1) converted number 16
and 81.3% answered correctly; 2) converted number 15 and 68.8% answered correctly;
3) converted number 10 and 68.8% answered correctly. The playful approach of DBOX was compared with the traditional approach (of the algorithm proposed above) in students of a fifth class where they were studying the powers of two. They starting using
D-BOX and then they used traditional method. Fifteen students, the same of before,
was asked, by the school teacher already trained about D-BOX, to convert number 4 all
students answered exactly (100% correct answers). Then, the students converted number
7 (which requires more attention because it is not an even number or a power of two),
87.5% answered correctly. Then, the students converted number 2 (which is a simple
question but it can be misleading) and 93.8% of the students answered correctly. Finally,
they converted number 25 (assuming an additional platform with 16 grooves to verify the
ability to extend the numbering) and 93.8% of the students answered correctly. To verify
the students’ ability to think about the concept of zero (essential for continuing their
mathematical studies after primary school), students had to convert the number 0 into its
binary equivalent (to do this, students had to leave all platforms empty) and 100% of the
children answered correctly. To test and verify students learning they converted a binary
number in its decimal equivalent. Numbers were: Bit5 Bit4 Bit3 Bit2 Bit1 Bit0 (with six
bits). The students converted the binary number 001112 into decimal, 81.3% of the pupils
answered correctly and 87.5% of the pupils converted 00001 correctly. After that they
used the traditional method to convert decimal number into binary numbers alone, they
converted: 1) 23 and 100% answered correctly; 2) 21 and 93.8% answered correctly; 3) 20
and 68.8% answered correctly. Comparing data, and taken into account that they convert
alone with no help from their teacher is quite motivating the improvement regarding the
conversion from decimal in binary numbers but there are still in students some problems
regarding the concept of zero.